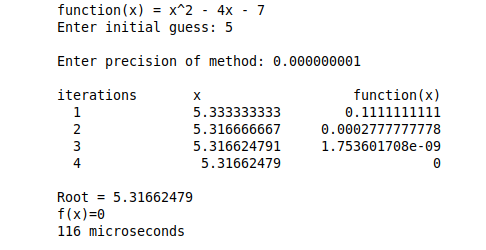
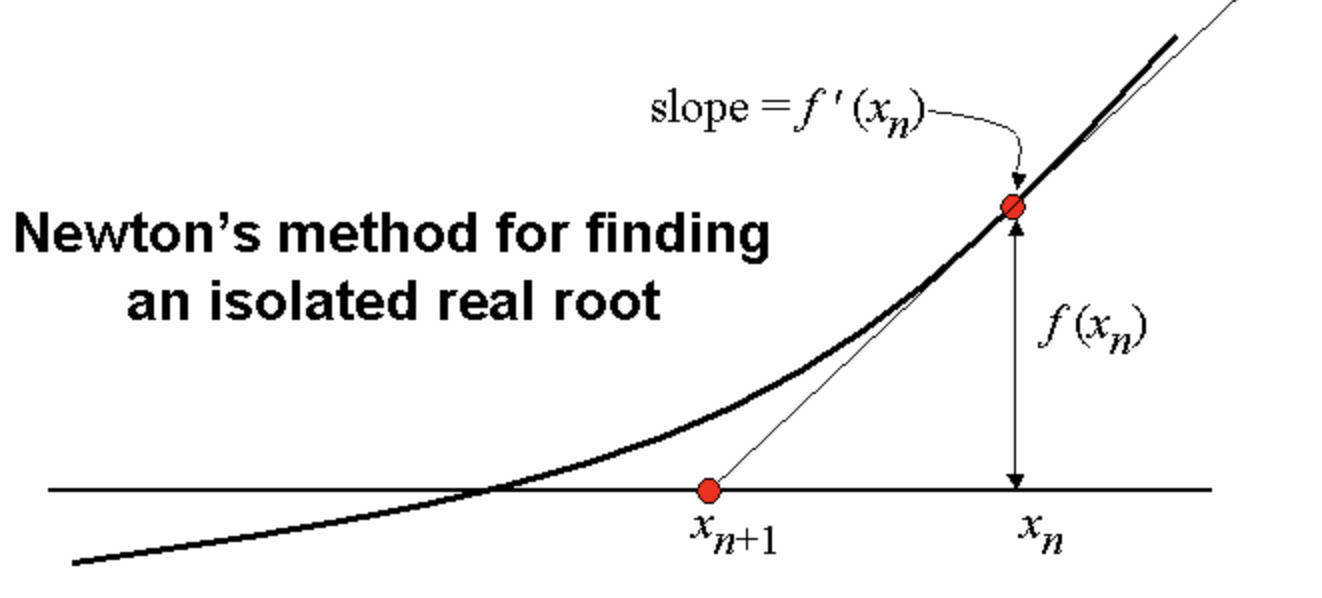
Newton raphson method example problems. Newton's Method (How To w/ Step 2023-01-05

Newton raphson method example problems Rating: 8,4/10 371 reviews

The Newton-Raphson method is a powerful and widely used technique for finding approximate solutions to equations. It is particularly useful for finding the roots of nonlinear equations, which cannot be solved using traditional algebraic methods. In this essay, we will explore the Newton-Raphson method through a series of example problems.

The basic idea behind the Newton-Raphson method is to iteratively improve an initial guess for the solution to an equation by using information about the slope of the equation at that point. This process is repeated until the solution is found to within a specified tolerance.

To illustrate the Newton-Raphson method, consider the equation x^2 - 3x + 2 = 0. This equation has two roots, x = 1 and x = 2. To find these roots using the Newton-Raphson method, we first need to rewrite the equation in the form f(x) = 0, where f(x) is a differentiable function. In this case, we can simply let f(x) = x^2 - 3x + 2.

Next, we need to choose an initial guess for the solution, which we will call x0. This initial guess should be reasonably close to the actual solution, as the Newton-Raphson method relies on the assumption that the function is well-behaved in the vicinity of the solution. In this example, we will choose x0 = 1.5.

Using the initial guess x0, we can then calculate the next approximation for the solution, x1, using the following formula:

x1 = x0 - f(x0) / f'(x0)

Where f'(x0) is the derivative of f(x) evaluated at x0.

Substituting the values from our example, we get:

x1 = 1.5 - (1.5^2 - 31.5 + 2) / (21.5 - 3)

= 1.5 - (-0.25) / (-0.5)

= 1.5 - 0.5

= 1

We can repeat this process to find the second root of the equation. Choosing x0 = 2, we get:

x1 = 2 - (2^2 - 32 + 2) / (22 - 3)

= 2 - (2) / (-1)

= 2 + 2

= 4

Since the solution x = 4 is not within the specified tolerance of the actual solution x = 2, we can repeat the process using x1 as the new initial guess. Continuing this process, we will eventually converge on the solution x = 2 to within the desired tolerance.

This simple example illustrates the basic principles of the Newton-Raphson method. In practice, the method can be applied to a wide range of equations, including those with multiple roots and those with more complicated functional forms. It is an essential tool for solving nonlinear equations, and is widely used in fields such as engineering, physics, and finance.

Calculus I

newton raphson method example problems

For the second iteration 4- Get the value of f 2. This search jumped to another root than the one closest to our starting point. We can clearly see that a plateau at 20 appears at the maximum value of our function and is there for the entire asymptotic region of the exponential tail. Well this seems like a "real world use" and i'll have to solve it first. Convergence plot Converged solution Codes A snapshot of the Mathematica code for both solved problems are shown below, along with the download links to the Mathematica notebook.

Next

6a

newton raphson method example problems

Think about the following situation: you tell me about some interesting phenomenon. At least, I learn more easily from examples. The relationship between x kand x k+1for a single-variable function f x reduces to FIGURE 18. So, if there are four roots, like in the previous example, there would be four colors. Therefore, we always need to check for this issue in the code. The boundary between these two regions of convergence vs.


Next

11 Highly Instructive Examples for the Newton Raphson Method

newton raphson method example problems

Now that might be a problem, because sometimes — finding the exact solution roots of an equation algebraically is easier said than done. The figures show that the iteration converges to a unique solution in 9 steps. Hey very sorry for the late reply, this tread just slipped my mind. As a result, running this as a numerical exercise can only help to expose missing maximum numbers of iteration, or producing numerical overflows. The result is getting closer to the actual root of our equation really quickly now. I guess that main thing I would like to know is where do we actually use a root of a number in engineering? Just imagine that you are computing a derivative of a function with two real variables instead of one.

Next

Newton Raphson Method

newton raphson method example problems

For this case, I show the third kind of plot again like in the first example , where the number of iteration steps needed for a solution is added to the overview. In our example, the origin is particularly unsuitable, because there the slope vanishes and so the Newton algorithm fails. You already got the idea from the first two with the concrete numbers and the illustrations. All of them are very close and it is hard to see anything: The function is plotted in blue and hard to see underneath the red-dashed tangents. Solve Problem 2 b , Set I8. I used Newtons method to compute shock polars for materials, does that help? The result is the following figure: These red dots indicate areas of fast convergence, where they are low, and slow convergence, where they are high. Use the Newton Method and give the answer to the nearest gram.

Next

Newton Raphson Method Practice Problems Online

newton raphson method example problems

Now what is that supposed to mean? This worked really well and fairly quickly, because we were close to the root and the function is well-behaved. One more step, ok? However, meaningful values are produced on the way to this failure, so we can still feel content about having avoided the asymptotic trap of this function. Numerically, in this particular example, the initial guess gets multiplied by a factor of negative two at each iteration step, growing geometrically beyond all bounds. Together we will walk through several examples, in great detail, so we can become human calculators and wield this new superpower. Find the break-even point of the firm, that is, how much it should produce per day in order to have neither a profit nor a loss. You are encouraged to use different initial x o to get a feel of how the method works.


Next

Real Work Application of Newthon

newton raphson method example problems

The Newton-Raphson method is an iterative procedure for solving simultaneous nonlinear equations. The process continues until two successive points, X k and X k +1 are approximately equal. Again, we can ask about the dependence of the number of necessary steps on the initial guess. In general, trial and error is used to locate a "good" initial point. Next, we will calculate the first derivative and substitute both the function and derivative into our formula. In particular, we see that around 30 iterations are needed to arrive at a converged result for the double root, while 5 or 6 suffice to get to a simple root with the same relative precision. It comes as is and without any warranty, so use at your own risk.

Next

Newton's Method (How To w/ Step

newton raphson method example problems

Here is the graph with the iteration path laid out by the red stars on the curves and the green Xs on the x-axis: I should mention here that converging towards a solution of zero as it happens here is a little problematic when defined via a relative difference. Above, we have used the function for computing the square root of two, because we know that its root is the number we want. That seems easy enough, right? Check out their domain offers here:. The first which root is translated into the color of the starting point on the grid, and the second how many iterations can be used to additionally shade the color of that point. Assume we want to find the root i. Solves the method for a given initial guess as well as tests the entire x grid as initial guesses Produces three figures: function overview tangents for chosen initial guess efficiency of other initial guesses Includes several presets for function, but is easily extendable author: Andreas Krassnigg, ComputingSkillSet. So when faced with solving an equation that seems impossible, we need this method! Can anyone give me some ideas on where this method could be used in say the "real world"? So, perhaps you do, too.

Next

Newton

newton raphson method example problems

Well it seems like a perfect real world engineering example but it would be fantastic if you could provide me with a simple example of doing that. The function we define for this purpose is can you guess it after having read the first example? For this, our usual plot with the number of necessary iterations as a function of the starting point comes in handy. The answer lies in the previous example. You can find it here: As you can see, this picture uses only color information and not shading — I leave the latter to the in-depth article linked above. We observe two things: to which root the method converges and how many iterations it takes to get there. Add your own as needed. Check it out here: My domain computingskillset.

Next