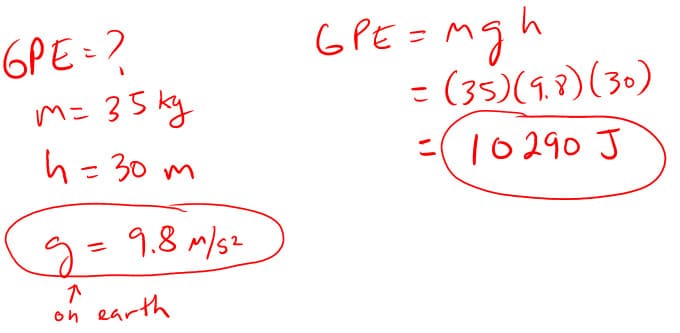Physics conservation of energy problems and solutions. 13.6: Conservation of Energy 2022-12-19

Physics conservation of energy problems and solutions Rating: 9,7/10 1312 reviews

The conservation of energy is a fundamental principle in physics that states that energy cannot be created or destroyed, but can only be converted from one form to another. This principle has numerous applications in various fields, including mechanics, thermodynamics, and electromagnetism. It is an essential concept in understanding the behavior of physical systems and predicting their future states.

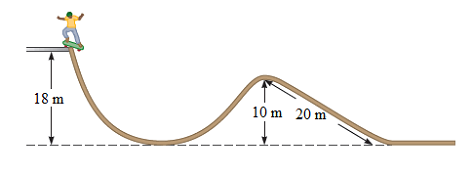
One of the key problems in physics that can be solved using the conservation of energy is the determination of the motion of an object. By understanding the total energy of a system, we can predict the motion of an object based on the forces acting on it. For example, if we know the kinetic energy (energy of motion) and potential energy (energy due to position) of an object, we can determine its speed and position at any given time.

Another application of the conservation of energy is in the field of thermodynamics, which deals with the transfer of heat and work in a system. The first law of thermodynamics, also known as the law of conservation of energy, states that the total energy of a closed system remains constant, regardless of the changes that may occur within the system. This principle is used to understand the behavior of heat engines, refrigerators, and other thermal devices.

There are also many practical problems that can be solved using the conservation of energy. For example, engineers can use the conservation of energy to design energy-efficient buildings and machines. By understanding the energy input and output of a system, engineers can optimize the design to minimize energy waste and improve efficiency.

One of the main challenges in applying the conservation of energy is accurately measuring and accounting for all the forms of energy present in a system. This can be particularly difficult when dealing with complex systems that involve multiple forms of energy, such as mechanical, thermal, and electrical energy. To accurately apply the principle of conservation of energy, it is necessary to carefully analyze the system and identify all the sources of energy and the ways in which they are converted.

In conclusion, the conservation of energy is a fundamental principle in physics that has numerous applications in various fields. By understanding the total energy of a system, we can predict the motion of an object, design energy-efficient machines and buildings, and solve a variety of practical problems. While the application of this principle can be challenging, it is an essential tool in understanding and predicting the behavior of physical systems.

Work and energy problems and solutions

physics conservation of energy problems and solutions

If the temperature of the thermal equilibrium is 36 o C, determine the mass of the copper! So the total energy of the bead —kinetic plus gravitational potential energy— will be conserved. Gravitational Potential Energy: The gravitational potential energy of an object is the energy it has because it has some height above some reference point in a gravitational field. How much did air resistance contribute to the dissipation of energy in this problem? Solution The mechanical energy dissipated by air resistance is the algebraic sum of the gain in the kinetic energy and loss in potential energy. Bobby compresses the spring1. Systems with a Single Particle or Object We first consider a system with a single particle or object. What is the minimum compression of the spring neccessary for the car to complete the loop without leaving the track? Steps for Solving Conservation of Energy Problems Step 1: Make a list of all known quantities given in the problem such as the object's mass, its initial and final height, and its initial and final speed. The reference points for the various potential energies do not have to be at the same location.

Next

Law of Conservation of Energy Problems with Solutions

physics conservation of energy problems and solutions

But we can use our result from Eq. At the final position A , the bead has both kinetic and potential energy. Until you learn more about the dynamics of systems composed of many particles, in. Step 1: We will first make a list of the known quantities given in the problem, including the mass of the block, its initial speed, and its initial and final height. Notice that we were able to calculate the energy dissipated without knowing what the force of air resistance was, only that it was dissipative. Answer: a Since the initial speed of the snowball is 20.

Next

8.3 Conservation of Energy

physics conservation of energy problems and solutions

It has velocity v and an impact parameter b the minimum distance between the centre of the sun and the extrapolation of the comet's initial path with respect to the Sun mass M. The engineers argued that Congress should force US Automakers to build this energy efficeint car. In It is sometimes convenient to separate the case where the work done by non-conservative forces is zero, either because no such forces are assumed present, or, like the normal force, they do zero work when the motion is parallel to the surface. Combining these three equations we can solve for V G. Find the angle θ. Try to do them before looking at the solution.

Next

Conservation of mechanical energy

physics conservation of energy problems and solutions

Therefore, we can imagine a progression of this transfer as the particle moves between its highest point, lowest point of the swing, and back to the highest point Figure 8. After the pile driver fell, the top of the nail was a height s 2 above the block. The illustration also includes the radius of curvature and height above the lowest point on the track for these locations. In these examples, we were able to use conservation of energy to calculate the speed of a particle just at particular points in its motion. If a non-conservative force e. With what frequency in hertz does it vibrate? Top sprinters also have a mass of about 80kg and can cover 100m in 10s.

Next

Conservation of Energy

physics conservation of energy problems and solutions

It falls onto the blob, catapulting the second stick figure into the air. When the mass crosses the equilibrium position, what is the speed of the mass? Use conservation of energy to find the speed of the object 2 when it hits the ground. . The first stick figure rolls the boulder off the edge of the platform. This increase in kinetic energy equals the decrease in the gravitational potential energy, which we can calculate from the geometry.

Next

Conservation of Mechanical Energy Problems and Solutions

physics conservation of energy problems and solutions

At what horizontal distance from the edge of the ledge does the man land? In the next part of the problem, we think about the forces acting on the bead at point A. This happens when the object moves from a certain height down to the ground. It would appear that vaulters have discovered a way to "violate" the law of conservation of energy. We can illustrate some of the simplest features of this energy-based approach by considering a particle in one-dimensional motion, with potential energy U x and no non-conservative interactions present. How much did air resistance contribute to the dissipation of energy in this problem? Conservation of Energy: In a conservative process, the total mechanical energy of a system stays constant.

Next

Conservation Problems And Solutions Worksheets

physics conservation of energy problems and solutions

What potential energy U x U x can you substitute in We will look at another more physically appropriate example of the use of Systems with Several Particles or Objects Systems generally consist of more than one particle or object. You may not use Newton's laws or the equations of motion to solve these problems. What is the velocity of a stone at a height of 15 m before it hits the ground? This means that whatever energy an object has lost in potential energy will be gained in kinetic energy. Was it the shoes? The velocity after falling 6 m is calculated from the equation of motion, d. But the method of analyzing particle motion, starting from energy conservation, is more powerful than that. Note that in section 2. Always look through our samples before starting doing your homework, as they can help you to deal with it successfully.

Next

Energy Problems

physics conservation of energy problems and solutions

Given these numbers, show that world record pole vaults would not be possible without the pole contributing some elastic potential energy. Determine the minimum height of the bridge L, that will allow her to stay dry that is, so that she stops just before hitting the water below. Assume that stick figures, boulders, and blobs obey the law of conservation of energy. On the following pages you will find some problems of work and energy with solutions. Hints And Answers For Energy Problems Hint and answer for Problem 2 The kinetic energy of the ball consists of translational and rotational kinetic energy. Discuss three natural cycles and their effects.

Next

Solved Example Problems for Law of conservation of energy

physics conservation of energy problems and solutions

Answer: a The condition of the pendulum when the stone passes the lowest point is shown in Fig. It is worth spending a bit of time on the analysis of a problem before tackling it. We reject the negative root. Be A man with a mass of 65 kg skis down a friction-less hill that is 4. The horizontal dimension has been foreshortened. Find the speed at height h. Answer and While you are reading our sample on the law of conversation of energy problems, you can get some ideas on how to deal with your own assignment.

Next