The great geometer. Euclid: The Great Geometer by Chris Hayhurst 2022-12-09
The great geometer
Rating:
9,4/10
332
reviews
The Great Geometer is a term that has been used to refer to a number of mathematicians throughout history who have made significant contributions to the field of geometry. Some of the most well-known Great Geometers include Euclid, Archimedes, and Riemann.
Euclid is perhaps the most famous Great Geometer of all time. He lived in ancient Greece around 300 BC and is known for his work on geometry, which he compiled in a textbook called "The Elements." This textbook became the standard for teaching geometry for over two thousand years and is still considered one of the most important works in mathematics. Euclid's work laid the foundations for much of the mathematics that we use today, including the concept of a proof, which he developed in order to rigorously prove the theorems that he presented in his textbook.
Archimedes was another famous Great Geometer who lived in ancient Greece around the same time as Euclid. He is known for his contributions to the field of calculus, which he used to solve problems related to geometry and physics. Archimedes is famous for his discovery of the principle of buoyancy, which states that an object will float if it is less dense than the fluid it is placed in. He also made significant contributions to the study of circles, cones, and spheres, and is known for developing the concept of the center of mass.
Riemann was a 19th century mathematician who made significant contributions to the field of geometry. He is known for his work on non-Euclidean geometry, which is a type of geometry that does not follow the same rules as traditional Euclidean geometry. Riemann's work on non-Euclidean geometry laid the foundations for the study of curved spaces and has had a significant impact on the fields of physics and cosmology.
In conclusion, the Great Geometers are a group of mathematicians who have made significant contributions to the field of geometry. Euclid, Archimedes, and Riemann are just a few of the many mathematicians who have earned this distinction, and their work continues to shape the way we understand and use geometry in the modern world.
The Great Geometer: Geometric Coloring Pages, Shapes and Patterns For Adults, Teens and Kids

Pg 1 6 Stewart, I. Then Christians would put forward the argument of design. Iona: The Earliest Poetry of a Celtic Monastery. Diameters and their conjugates are defined in Book I Definitions 4—6. The headings, or pointers to the plan, are somewhat in deficit, Apollonius having depended more on the logical flow of the topics. Since the first moon landing in 1969 Torensma breaks a lance for life and its inherent special macro- and micro-cosmic processes, of which we are hardly aware in daily life. Apollonius believed Euclid needed the theorems he presented in book three in order to complete many of his proofs.
Next
"The Great Geometer", Apollonius

. Scholars of the 19th and earlier 20th centuries tend to favor an earlier birth, 260 or 262, in an effort to make Apollonius more the age-mate of Archimedes. Apollonius claims original discovery for theorems "of use for the construction of solid loci. It cut both cones of the pair, thus acquiring two distinct branches only one is shown. Santa Fe, NM: Green Lion Press.
Next
The great Geometer

Arbeiten zur Fruhmittelalterforschung, 17. Book VI features a return to the basic definitions at the front of the book. Book seven explains determinative theorems, and book eight provides some theorems determined in this way. It can have any length. Introduction God- The Great Geometer Since the dawn of mathematics, humans have tried to use it's methods to answer this question: What are we, and everything around us, made of? Thought and Letters in Western Europe: A. This would be circular definition, as the cone was defined in terms of a circle. Apollonius might be remembered by The Conics but it is not only his work.
Next
Apollonius of Perga

With his work he influenced many other mathematicians that came after him, one of which isJohannes Kepler. He also traveled to Pergamum. This coloring book offers a broad variety of designs suited for all skill levels - ranging from beginner to expert level. Its plane is parallel to a side in the conic surface of the axial triangle. The most difficult and historically interesting case arises when the three given things are circles.
Next
Virgil of Salzburg

It also has large The topic is relatively clear and uncontroversial. There are subtle variations in interpretation. Torensma uses natural pigments which he applies on a surface of quartz crystals. Godbid, voeneunt apud Robertum Scott, in vico Little Britain. Around 350 BC, the ancient Greek philosopher Plato, in his book Timaeus, theorized that these four elements were all aggregates of tiny solids in modern parlance, atoms.
Next
God

Apollonius studied mathematics at the great University and Library in Alexandria under the successors of the great mathematical encyclopaedist Euclid. Its plane is parallel to the axis. Retrieved 15 May 2020. Even as recently as 1956, Paul Dirac, one of the founders of quantum mechanics, wrote "a physical law must possess mathematical beauty"5 When it Conclusion We like easy and straightforward patterns. Apollonius of Perga lived from approximately 262 B.
Next
The Great Geometer

In Apollonius' definitions at the beginning of Book VI, similar right cones have similar axial triangles. Humans attempt to comprehend the intricate geometry in nature, and each time a new type is discovered, we attempt to handle it, and point out imperfections- but god accepts them without doubt. Is God a Geometer? He works essentially only in Quadrant 1, all positive coordinates. Obversation: I don't know but some times when mathematicians or historians discuss the mathematics or science in history they tend to downplay or ignore contributions outside of Gree About this book: This is not a review, because there's really not much information about Euclid the man. Accedunt ejusdem de sectione spatii libri duo restituti in Latin.
Next
Euclid : the great geometer : Hayhurst, Chris : Free Download, Borrow, and Streaming : Internet Archive

. Relationships not readily amenable to pictorial solutions were beyond his grasp; however, his repertory of pictorial solutions came from a pool of complex geometric solutions generally not known or required today. Until recently Heath's view prevailed: the lines are to be treated as normals to the sections. In these Apolloniusdiscusses normals to conics and shows how many can be drawn from a point. Hearing of this plan from Apollonius himself on a subsequent visit of the latter to Pergamon, Eudemus had insisted Apollonius send him each book before release. He intended to verify and emend the books, releasing each one as it was completed.
Next
Apollonius

The Conics completely summarized the existing knowledge and also extended the knowledge of conic sections. Some people believe that there is no evidence that the something that started the chain of movement off was God. Prefaces IV—VII are more formal, omitting personal information and concentrating on summarizing the books. Each figure has its own geometric definition, and in addition, is being shown to be a conic section. Being the most stable of the elements, earth must consist of cubes.
Next
List of geometers
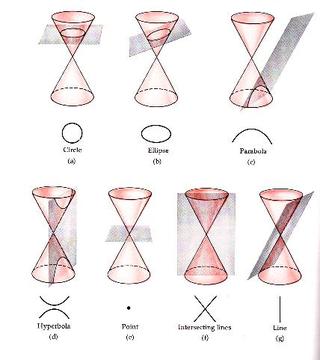
Heath's work is indispensable. These translations became part of the Encyclopædia Britannica's Contemporaneously with Taliaferro's work, Heath, Taliaferro, and Thomas satisfied the public demand for Apollonius in translation for most of the 20th century. These are not code words for future concepts, but refer to ancient concepts then in use. . This book takes readers into Euclid's life, and to the ancient Greece in which he was raised, with full-color and black-and-white images, many of which are primary sources. The Greek geometers were interested in laying out select figures from their inventory in various applications of engineering and architecture, as the great inventors, such as Archimedes, were accustomed to doing. The ambiguity has served as a magnet to exegetes of Apollonius, who must interpret without sure knowledge of the meaning of the book's major terms.
Next








