Van hiele theory. Teaching Geometry for a Deeper Understanding 2023-01-01

Van hiele theory Rating: 9,8/10 320 reviews

The Van Hiele theory, also known as the Van Hiele model or the Van Hiele levels of geometric thinking, is a theory of mathematical development that was proposed by two Dutch educators, Dina van Hiele-Geldof and Pierre van Hiele. The theory is based on the idea that students progress through a series of levels as they develop their understanding of geometry, and that these levels are hierarchical, with each level building upon the understanding and skills acquired at the previous level.

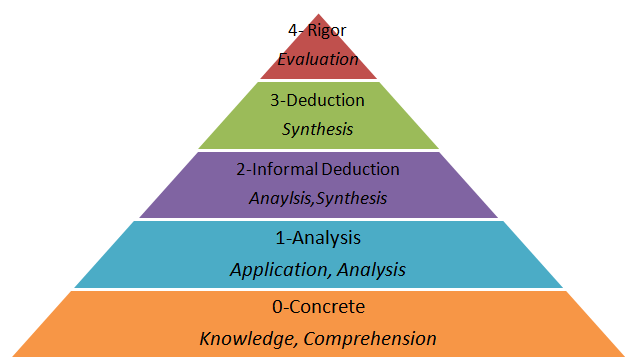
According to the Van Hiele theory, there are five levels of geometric thinking, each corresponding to a different stage of development. These levels are:

  1. Visualization: At this level, students are able to recognize and draw basic geometric shapes, such as circles, squares, and triangles. They are able to identify these shapes in their environment and distinguish between them based on their characteristics, such as size and number of sides.

  2. Analysis: At this level, students are able to classify shapes based on their properties, such as size, symmetry, and angles. They are also able to recognize and describe the relationships between shapes, such as congruence and similarity.

  3. Deductive: At this level, students are able to use logical reasoning to prove geometric statements and theorems. They are able to apply their understanding of geometric concepts to solve problems and make predictions.

  4. Informal Deductive: At this level, students are able to apply their understanding of geometry in more abstract and formal settings, such as in coordinate geometry and transformations.

  5. Formal Deductive: At this highest level, students are able to apply their understanding of geometry in more complex and abstract settings, such as in non-Euclidean geometries.

The Van Hiele theory suggests that students typically progress through these levels in a linear fashion, with each level building upon the understanding and skills acquired at the previous level. However, the rate at which students progress through the levels can vary greatly, and some students may never reach the highest levels of geometric thinking.

One of the key implications of the Van Hiele theory is that teaching geometry should not be limited to simply memorizing formulas and theorems, but should instead focus on helping students develop their understanding of geometric concepts and their ability to apply them in real-world situations. This can be achieved through activities such as hands-on exploration, problem-solving, and the use of visual aids and manipulatives.

In conclusion, the Van Hiele theory is a valuable framework for understanding the development of mathematical thinking, particularly in the area of geometry. By recognizing the different levels of geometric thinking and the skills and understanding that students acquire at each level, educators can tailor their instruction to meet the needs and abilities of their students, and help them progress through the levels of geometric thinking in a meaningful and effective way.

Van Hiele Model

van hiele theory

Seventy-first yearbook, Reston, VA: National Council of Teachers of Mathematics, pp. When you're looking for a set of shapes, think about what might be tricky about an attribute For example right angles are harder to see if they aren't horizontal and vertical--if your sorting attributes include right angles, you want some tilted ones in your sorting set. A student can now see how one figure could be described in different ways if it shares the same properties as another figure. In: Lesh R, Mierkiewicz D eds Recent research concerning the development of spatial and geometric concepts. Basically, they will see geometry in the abstract. Those who fall behind will only be able to memorize and scrape by.

Next

Teaching Geometry for a Deeper Understanding

van hiele theory

Construct some more rhombi on your paper. How do they work? Deduction: Students at this level understand the meaning of deduction. Students cannot "skip" a level. Children at this level may describe and define a shape by listing a lot of the properties that the shape has parallelograms have opposite sides that are parellel and have the same length, their opposite corners have the same angle. Thought Process: This figure has two pairs of congruent sides, so it could be a rectangle or maybe a parallelogramā€¦. A student in this level will know that parallelograms have opposite sides that are parallel and will be able to group them accordingly.

Next

Description of the Van Hiele theory

van hiele theory

Children will have enough experience with geometry definitions that they know what sorts of attributes are used in geometry definitions, and what sort aren't considered important properties of shapes. At Level 0 a square is something that looks like a box. Unpublished doctoral Dissertation, University of Georgia. It can seem like a grueling task to teach and to learn. Some researchers syncretic level.

Next

Van Hiele model

van hiele theory

As it goes with most learning, the earlier the better. Detailed accounts and summaries of this early, but still highly relevant, work can be found in the following: Clements and Battista The Theory has two main aspects that combine to provide a philosophy of mathematics education not only of Geometry. We do not learn enough about pi, spheres, and symmetries. There have been many teachers who have attempted to make the formal understanding easier with new programs and methods. Because of the inability to understand definitions which are based on the properties of the figures , the student at this level is not able to, for example, recognise a square as a special case of a rectangle. Another thing to keep in mind is that all the language and vocabulary that you use has to match the particular student level.

Next

The van Hiele Theory

van hiele theory

In this study, all references made to research studies that used the level 0 to 4 numbering system have been modified to the level 1 to 5 numbering system. He has not learned to establish connections between the system and the sensory world. Furthermore, since the majority of high school geometry courses are taught at level 3, it is not surprising that most research has also concentrated on lower levels. The teacher may give the students an overview of everything they have learned. Neither of these is a correct description of the meaning of "square" for someone reasoning at Level 1. Knowing that properties are important is something children learn by discussing and working with properties.

Next

van Hiele Theory, The

van hiele theory

Set diagrams are helpful for showing relationships between different kinds of shapes. The model has greatly influenced geometry curricula throughout the world through emphasis on analyzing properties and classification of shapes at early grade levels. It startedas a high school project but the 6th graders caught on quickly. I would recommend initially starting with sorting by property and not by name, and attaching the name to the group after sorting this means that children focus on the property and aren't distracted by their visual examples of the named group. It has a bunch of activities, games, proofs, inquiry lessons, challenges, etc. Each hour it could go from easy to more difficult. Academic, New York Cite this entry Pegg, J.

Next

properties of triangles and quadrilaterals

van hiele theory

The van Hieles believed this property was one of the main reasons for failure in geometry. We know that our brains develop in stages. This should result in squares being included in the rectangle group 4 right angles and rectangles and squares being sorted in the parallelogram group 2 parallel sets of sides etc. For example, it is sufficient for a figure to have four sides if it is to be identified as a quadrilateral but it is necessary for all the sides to be equal in length for it to be a square or a rhombus and it is necessary that all four angles be right angles for it to be a square. Level 0: Visualization Children start out at a visualization level of understanding geometry and thinking about shapes.

Next

The Van Hiele Student Development Levels for Geometry Learners

van hiele theory

Problems may be more complex and require more free exploration to find solutions. Challenges: The student may have difficulty progressing from one property to another. This task strengthens students understanding of what rules can be used to define a set of shapes. In: Grimison L, Pegg J eds Teaching secondary mathematics: theory into practice. The Van Hiele levels have helped shaped curricula throughout the world, including a large influence in the standards of geometry in the US. Students without basic knowledge or the ability to back up statements with reason are easily set up to fail in class.

Next