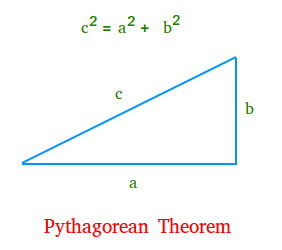
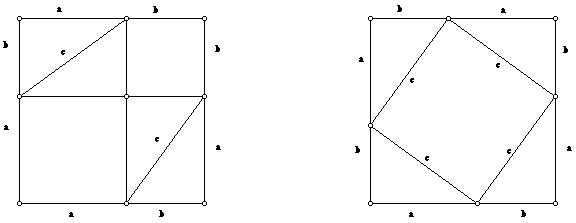
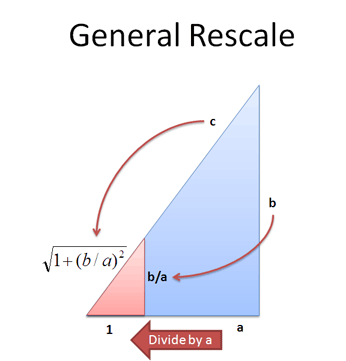
Who created the pythagorean theorem. Who Invented The Pythagorean Theorem? 2022-12-07

Who created the pythagorean theorem Rating: 6,4/10 1431 reviews

The Pythagorean theorem is a mathematical concept that states that in a right triangle, the square of the length of the hypotenuse (the side opposite the right angle) is equal to the sum of the squares of the other two sides. It is expressed as the equation a^2 + b^2 = c^2, where c is the length of the hypotenuse and a and b are the lengths of the other two sides. This theorem is an important concept in geometry and is widely used in many areas of mathematics and engineering.

The origins of the Pythagorean theorem can be traced back to ancient civilizations, where it was known by different names and used for various purposes. However, it was the Greek mathematician Pythagoras who is credited with formally stating and proving the theorem.

Pythagoras was born on the island of Samos in the Aegean Sea around 570 BCE. He was a philosopher, mathematician, and scientist who founded a religious and philosophical movement known as Pythagoreanism. One of the main beliefs of this movement was that mathematics was the key to understanding the universe and that numbers had a mystical significance.

Pythagoras is known for his work on geometry, particularly the theorem that bears his name. Although the theorem was known to ancient civilizations before Pythagoras, he was the first to prove it rigorously and to give it a formal statement. In his proof, he used the concept of similar triangles, which states that two triangles are similar if they have the same angles. By showing that the ratios of the sides of similar triangles are always the same, Pythagoras was able to prove the theorem.

In addition to his work on the Pythagorean theorem, Pythagoras made many other important contributions to mathematics and science. He is known for his work on the concept of irrational numbers, which are numbers that cannot be expressed as a ratio of integers. He also made important contributions to the study of music and acoustics, and is credited with discovering the mathematical relationship between the lengths of strings and the pitches they produce.

Despite his many contributions, Pythagoras is best known for the theorem that bears his name. The Pythagorean theorem has been a fundamental concept in mathematics for more than two thousand years, and it continues to be an important tool in many fields today. It is a testament to the enduring legacy of Pythagoras and his contributions to the world of mathematics.

The Controversial Origins Of The Pythagorean Theorem

who created the pythagorean theorem

Pythagoreans also claimed that Pythagoras possessed supernatural gifts. Within the big square on the left side, the four triangles are moved to form two similar rectangles with sides of length a and b. The first calculation of π was done by Archimedes of Syracuse 287—212 BC , one of the greatest mathematicians of the ancient world. Pi is an irrational number, which means that it is a real number that cannot be expressed by a simple fraction. Why is Pythagoras theorem named after him? Pythagoras was the first person to realise why that ratio amongst others worked.


Next

Pythagoras Theorem

who created the pythagorean theorem

Plimpton 322 is a systematic study of this zoo to discover the useful shapes," Mansfield said, referring to the fact that different types of right triangles can have different interior angles. Therefore, the parallelogram BL is equal to the square GB. Because angle BAC and angle BAG are right angles, lines CA and AG form a straight line. Because object projections can overlap on a coordinate subspace, the measure of each object projection in the set must be calculated individually, then measures of all projections added together to provide the total measure for the set of projections on the given coordinate subspace. What is the formula for Pythagorean? He did not leave a proof, though.

Next

Who discovered Pythagorean theorem first?

who created the pythagorean theorem

Selected works of Wen-tsün Wu. If x is increased by a small amount dx by extending the side AC slightly to D, then y also increases by dy. } The Pythagorean theorem, valid for right triangles, therefore is a special case of the more general law of cosines, valid for arbitrary triangles. } This can be considered as a condition on the cross product and so part of its definition, for example in Generalizations Similar figures on the three sides The Pythagorean theorem generalizes beyond the areas of squares on the three sides to any If one erects similar figures see This extension assumes that the sides of the original triangle are the corresponding sides of the three congruent figures so the common ratios of sides between the similar figures are a:b:c. They understood the relationship between the sides of a right-angled triangle.


Next

Who created the Pythagorean Theorem?

who created the pythagorean theorem

New York, New York: Springer-Verlag New York, Inc. The Pythagorean Theorem: One of the most well-known theorems in mathematics and geometry is the Pythagorean Theorem. Also, we will learn how to prove it using various methods. Pythagoras Nevertheless, the theorem came to be credited to Pythagoras. Roots to research: a vertical development of mathematical problems. Despite this soggy piece of history, Pythagoreans did introduce more rigorous mathematics to ancient Greece. Instead, in the margin of a textbook, he wrote that he knew that this relationship was not possible, but he did not have enough room on the page to write it down.

Next

Who invented Pythagoras theorem? + Example

who created the pythagorean theorem

Pythagorean triples Babylonian scribes van der Waerden. In addition, we also draw the lines AD and FC. Mathematical Association of America. States that in a right triangle that, the square of a a2 plus the square of b b2 is equal to the square of c c2. However, the relationship was not widely publicized until Pythagoras stated it explicitly. A Commentary of the First Book of Euclid's Elements.

Next

How old was Pythagoras when he discovered the Pythagorean Theorem?

who created the pythagorean theorem

The view of Pythagoras's cosmos sketched in the first five paragraphs of this section, according to which he was neither a mathematician nor a scientist, remains the consensus. Plimpton Collection at Columbia University. Some ancient clay tablets from Babylonia indicate that the Babylonians in the second millennium B. How old was Pythagoras when he discovered Pythagoras theorem? Mathematical methods for physicists: a concise introduction. However, the left green parallelogram also has the same area as the left green parallelogram of the upper figure, because they have the same base the upper left side of the triangle and the same height normal to that side of the triangle. Geometrically r is the distance of the z from zero or the origin O in the This can be generalised to find the distance between two points, z 1 and z 2 say.

Next

Pythagorean History

who created the pythagorean theorem

Its useful right angles are everywhere, whether it is a building, a table, a graph with axes, or the atomic structure of a crystal. Proof using similar triangles This proof is based on the Let ABC represent a right triangle, with the C, as shown on the figure. Princeton, New Jersey: Princeton University Press. The distance formula in Cartesian coordinates is derived from the Pythagorean theorem. Acta Historica Scientiarum Naturalium et Medicinalium. He carried out important research in partial differential equations of the first order and applied them to the differential equations of dynamics.

Next

Pythagorean theorem

who created the pythagorean theorem

Other uses of trigonometry: It is used in oceanography in calculating the height of tides in oceans. A portion of a 4000 year old Babylonian tablet c. Mathematics is one of the ancient sciences developed in time immemorial. It remains one of the most widely known, with more than 400 different proofs existing today, covering everything from algebra to geometry. The Pythagorean proposition 2nded.

Next

Who really invented the Pythagorean theorem?

who created the pythagorean theorem

English mathematician Algebraic proofs The theorem can be proved algebraically using four copies of the same triangle arranged symmetrically around a square with side c, as shown in the lower part of the diagram. In the first column the OBs encode an entire Pythagorean Triple as a single decimal actually sexagesimal, they used base 60 number between 1 and 2. Who was Pythagoras and his contribution in mathematics? In 2017, Mansfield had discovered a tablet from the same period, named Plimpton 322, which he identified as containing another trigonometric table. His followers gained a reputation for secrecy. Maybe this odd choice of first column is really in the middle of the tablet.

Next