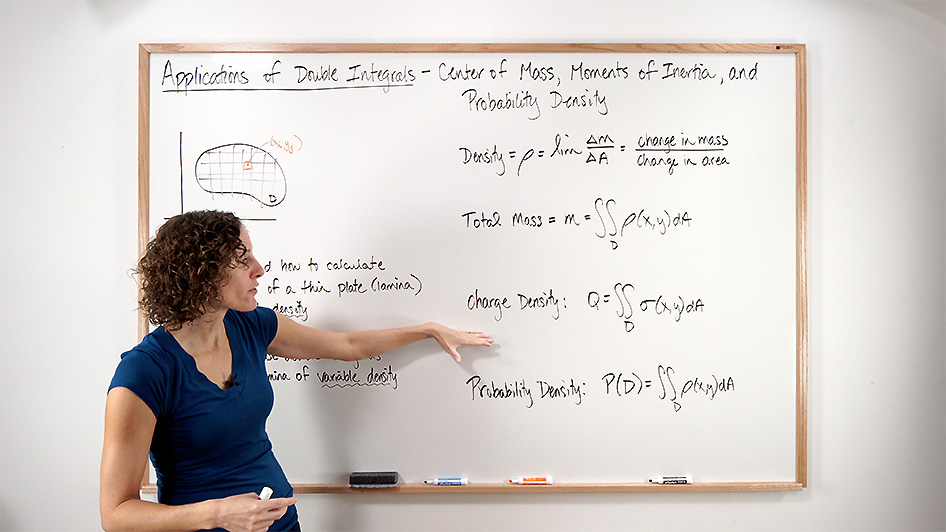
Applications of multiple integrals in real life. Physical Applications of Triple Integrals 2022-12-14

Applications of multiple integrals in real life Rating: 5,7/10 1565 reviews

Multiple integrals are a powerful mathematical tool that can be used to solve a wide range of problems in the real world. In this essay, we will explore some of the key applications of multiple integrals in various fields.

One of the most common applications of multiple integrals is in the field of engineering and physics. Engineers often use multiple integrals to solve problems related to the analysis and design of systems, such as the stress and strain in a structure or the flow of fluids through a pipe. For example, in civil engineering, multiple integrals can be used to calculate the volume of a solid, the moment of inertia of a beam, or the surface area of a curved surface. In mechanical engineering, multiple integrals can be used to analyze the forces and moments acting on a system, such as the lift and drag forces on an aircraft or the torque on a motor shaft.

Multiple integrals are also widely used in the field of economics and finance. For example, they can be used to calculate the present value of an investment or the cost of capital for a company. They can also be used to analyze the market demand for a product or the supply of a particular resource. In addition, multiple integrals can be used to model the behavior of financial markets and to develop financial instruments such as options and futures contracts.

Multiple integrals are also used in the field of computer science and programming. They can be used to solve problems related to image processing, computer graphics, and machine learning. For example, multiple integrals can be used to analyze the performance of algorithms, to optimize the layout of a website, or to design the structure of a database. They can also be used to develop software programs and applications, such as computer games, web browsers, and mobile apps.

Multiple integrals are also used in the field of biology and medicine. They can be used to model the distribution of drugs in the body, to study the spread of diseases, or to analyze the behavior of cells and tissues. In addition, multiple integrals can be used to develop medical devices and technologies, such as drug delivery systems, imaging systems, and diagnostic tools.

In conclusion, multiple integrals are a powerful and versatile mathematical tool that has a wide range of applications in the real world. They are used in a variety of fields, including engineering, physics, economics, finance, computer science, programming, biology, and medicine. Multiple integrals are an essential tool for solving complex problems and making informed decisions in the modern world.

5 Real

applications of multiple integrals in real life

We will compute the double integral by first computing and we compute this by holding x constant and integrating with respect to y as if this were an single integral. This can be done through various differential equations. Students can learn how to control a system by studying calculus. Finding a Volume Under the Surface Finding the areas of bounded regions is one of the more basic applications of double integrals, but moving into a higher dimension also allows us to explore volume. Definite integrals are defined for integrals with limits and indefinite integrals do not include any limits. Let us have a look at one of the common applications of integrals i.

Next

Physical Applications of Triple Integrals

applications of multiple integrals in real life

Our double integral now becomes: Note that we can also use double integrals for finding areas of bounded regions that form more complex shapes, which may not be as familiar as rectangles or triangles. Q2: What are the 4 concepts of calculus? Your best friend is someone who understands you and knows how to make you laugh. A best friend is someone with whom you have a strong emotional connection. The indefinite integrals are used to integrate the algebraic expressions, trigonometric functions, logarithmic, and exponential functions. Ans: In Economics, calculus is used to compute marginal cost and marginal revenue, enabling economists to predict maximum profit in a specific setting. Differential calculus deals with the process of dividing something to understand or calculate the changes.

Next

15.4: Applications of Double Integrals

applications of multiple integrals in real life

How Do You Define Integration? Our inner integral is now: The double integral becomes: The limits on the outer integral which uses the numerical limits of the region rather than curves are the numerical boundaries for the variable y. There are two forms of integrals. As a double integral: Similarly, the first moment about the y-axis is given by: In addition to first moments, we can calculate second moments I x and I y. If you use a double integral, you can do 2 dimensional shapes defined by curves, and a triple integral lets you do a 3d shape defined by curves. If a body rotates about an axis which does not coincide with a principal axis of inertia, it will experience vibrations at the high rotation speeds. Thus, area multiplied by surface density has dimensions of mass M.

Next

Applications of Double Integrals

applications of multiple integrals in real life

Differentiation is the process by which the rate of change of a curve is determined. Iterated Integrals So far, we have seen how to set up a double integral and how to obtain an approximate value for it. Finding the Area of a Bounded Region Look at a rectangle, of length 4 and width 2, in the x- y plane. As long as we're careful about defining the limits for the inner and outer integrals, we can follow the same general steps to find the area. A classic example is velocity and displacement. You fundamentally cannot avoid integrals if you want to do anything meaningful with physics. .

Next

Real Life Applications of Calculus: Areas of Usage

applications of multiple integrals in real life

We have two integrals to denote the fact that we are dealing with a two dimensional region and we have a differential here as well. In this section we investigate double integrals and show how we can use them to find the volume of a solid over a rectangular region in the xy-plane. An integral is a function, of which a given function is the derivative. The most common type of integral is the definite integral, which is used to calculated the area under a curve. Integration is used to find out areas, volumes, and central points.

Next

Application of Integrals

applications of multiple integrals in real life

The next topic of this section is a quick fact that can be used to make some iterated integrals somewhat easier to compute on occasion. In mathematics, double integrals enable the process of integration in two-dimension areas. READ : 8 Fun Activities For Improving Situational Awareness In Kids After which the slope descends steeply. Notice how we use properties i and ii to help evaluate the double integral. We fix a y and look at which curves bound the x values.

Next

Tell me real life applications of integrals : learnmath

applications of multiple integrals in real life

Business One of the most common applications of derivatives of differentiation is when data is computed on a graph or a data table like an Excel sheet. Note that the formulas for the curves have been rewritten so that x is the subject. This is one of the most crucial instances of real-life applications of differentiation. Here is another example to illustrate this concept. If you give me only acceleration, I can tell you how fast the object was moving and how far it went.


Next

Applications of Multiple Integrals in Engineering

applications of multiple integrals in real life

Instead we have the R written below the two integrals to denote the region that we are integrating over. You could integrate the function of how fast material passes through over the shape of the pipe's cross section to figure out how fast material comes out of the end overall. Second moments are called moments of inertia. Now, when we derived the definition of the definite integral we first thought of this as an area problem. Thus, at the origin, the surface height is 2. To get a better estimation of the volume we will take n and m larger and larger and to get the exact volume we will need to take the limit as both n and m go to infinity.

Next

Double Integrals: Applications & Examples

applications of multiple integrals in real life

Let's consider a square in the x- y plane. This leads to integrating an integrand which is itself an integral. Further, for the calculation of areas or irregular shapes in a two-dimensional space, we use majorly integrals formulas. There are several variables that go into this calculation. This person is someone you can trust and confide in.

Next

Applications of Multiple Integrals in Engineering

applications of multiple integrals in real life

They are used in the field of graphical representation, where three-dimensional models are demonstrated. What if we change the order of the differentials? Therefore, when designing such devices it is necessary the axis of rotation to be coinciding with one of the principal axes of inertia. Except this equation only makes sense when F is constant, and usually it isn't. Double integrals work in the same manner. Economics Differential calculus is used in economics to calculate marginal cost, marginal revenue, maxima, and minima, and also enables economists to predict maximum profit or minimum loss in specific conditions.

Next