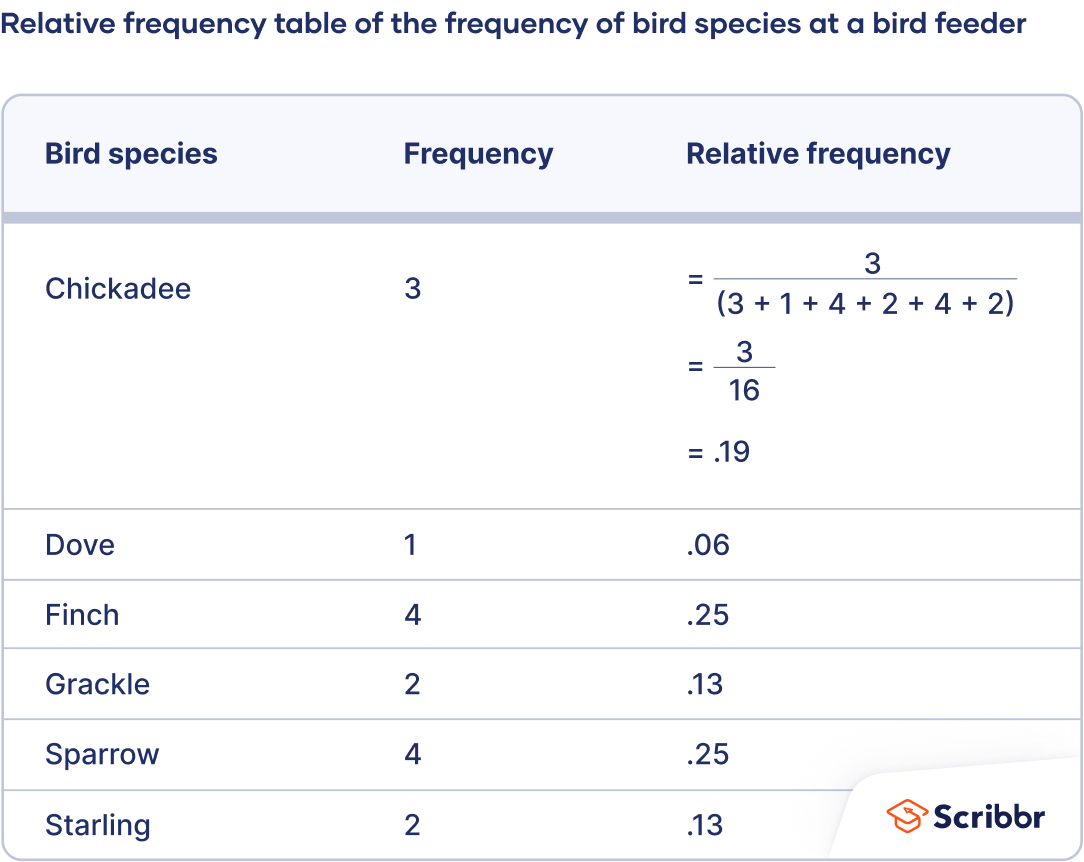
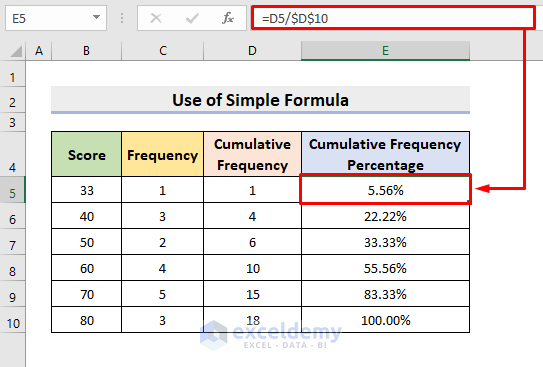
Cumulative frequency distribution example. Cumulative Distribution Function Example 2023-01-06

Cumulative frequency distribution example Rating: 4,3/10 1983 reviews

A cumulative frequency distribution is a type of frequency distribution that shows the total number of observations that fall below each value in a set of data. It is often used to visualize the distribution of a continuous variable, such as height or weight, and can be helpful in understanding the underlying patterns in the data.

One example of a cumulative frequency distribution is a graph showing the distribution of heights among a group of individuals. To create this graph, we would first measure the height of each person in the group and then sort the data from lowest to highest. Next, we would plot the heights on the x-axis and the cumulative frequency on the y-axis. The cumulative frequency is calculated by adding up the frequencies of each value as we move from left to right on the x-axis.

For example, let's say we have a group of 10 people with the following heights:

5'3", 5'4", 5'5", 5'6", 5'7", 5'8", 5'9", 5'10", 5'11", 6'0"

We would first sort the data from lowest to highest:

5'3", 5'4", 5'5", 5'6", 5'7", 5'8", 5'9", 5'10", 5'11", 6'0"

Then, we would plot the heights on the x-axis and the cumulative frequency on the y-axis. The cumulative frequency for each height is calculated by adding up the frequencies of all the previous heights. For example, the cumulative frequency for 5'7" would be the sum of the frequencies of 5'3", 5'4", 5'5", and 5'6".

Here is what the cumulative frequency distribution graph would look like:

Height (x-axis)Cumulative Frequency (y-axis)
5'3"1
5'4"2
5'5"3
5'6"4
5'7"5
5'8"6
5'9"7
5'10"8
5'11"9
6'0"10

From this graph, we can see that the majority of the individuals in this group are between 5'7" and 5'11" in height. We can also see that there is a relatively small number of individuals who are shorter or taller than this range.

Cumulative frequency distributions can be useful in a variety of contexts, such as when we want to compare the distribution of a continuous variable across different groups or when we want to understand the distribution of a continuous variable within a single group. They can also be helpful in identifying outliers or unusual values in the data.

In conclusion, cumulative frequency distributions are a useful tool for visualizing the distribution of a continuous variable and understanding patterns in the data. They can be helpful in a variety of contexts and can provide valuable insights into the underlying patterns in the data.

Cumulative Distribution Function Example

cumulative frequency distribution example

As the grade levels progress from low to high, the orange line rises to the total number of students, 88. Generally, a frequency distribution graph consists of an X-axis horizontal line that contains the categories or set of scores arranged in increasing order from left to right. CDF at negative infinity is equal to zero, at infinity its value is equal to 1 and it can never decrease. For example, no values repeat in the portion of the height data below. The frequency of a value is the number of times it occurs in a dataset. Cumulative frequency distribution is a form of frequency distribution that is created to represent the sum of the frequencies of a class and all classes below.

Next

What is frequency distribution in statistics with example?

cumulative frequency distribution example

On joining these points successively by smooth curves, we get a curve known as a cumulative frequency curve or an ogive. Frequency distributions allow them to see the bigger picture of the data. What are the various types of frequency distribution? These are actual data from a study I conducted involving preteen girls. The last value will always be equal to the total for all observations since all frequencies will already have been added to the previous total. By summing the current and previous rows, you calculate the running total. Hence, we know there are 88 students in this dataset. Note: A sigma Σ denotes frequency.


Next

How To Find Cumulative Frequency? (w/ 11 Examples!)

cumulative frequency distribution example

Percentiles If you recall, the summary measure that divides a ranked data set i. A bar chart is a good choice when you want to compare the frequencies of different values. And percentiles indicate the percentage of observations a value is above. Cumulative frequency is plotted on the vertical axis and class boundaries are plotted on the horizontal axis. Hence we will straight away move to step 3.

Next

Frequency Distribution: Types & Examples

cumulative frequency distribution example

What are the different shapes of frequency distributions? The upward cumulation result is more than or greater than the cumulative curve. Ans: The cumulative frequency of a class interval is the sum of frequencies of all the classes up to the specified class interval. What is the cumulative distribution function formula? Quantitative data which we exactly need is collected by statistics and it improves our research. To calculate the relative frequencies, add each frequency to the frequencies in the previous rows. That is, they can detect any patterns unnoticed within the frequency distribution.

Next

Cumulative Distribution Function

cumulative frequency distribution example

The cumulative frequency here starts from the frequency of the first class interval and ends at the maximum frequency. More than 0-20 4 4 18 total 20-40 5 9 4 + 5 14 18 - 4 40-60 6 15 9 + 6 9 14 - 5 60-80 3 18 15 + 3 3 9 - 6 Less than curve or ogive: Mark the upper limits of class intervals on the x-axis and take the less than type cumulative frequencies on the y-axis. But, instead of using 219, the endpoint of 320 is used. An ogive is a freehand graph showing the curve of a cumulative frequency distribution. For example, We use the same example as above and create a Less than Cumulative Frequency Distribution table. The ogive shows at what percent of the data is below a particular value. In this case, frequencies are counts of how often continuous data fall within each class.

Next

Cumulative Frequency Distribution, Definition, Formulas

cumulative frequency distribution example

A cumulative frequency distribution shows the cumulative frequency of each class. This will shift the center and location mean, median, mode, quartiles, and percentiles of the distribution that amount, but the shape and spread of the distribution range, IQR, and standard deviation will not change. Cumulative Frequency Cumulative frequency is the total of a frequency and all frequencies in a frequency distribution until a certain defined class interval. It's not mandatory to draw a graph, but a graphical representation of the data not only helps to show the trend of that particular question but also it helps to find the mean and the median in a distinctive way. The Daily Income of Workers in rupee No. Let us look at an example: Example: A car dealer wants to calculate the total sales for the past month and wants to know the monthly sales in percentage after weeks 1, 2, 3, and 4. Cumulative frequency is the sum of all the frequencies until we determine the data according to a class interval.

Next

Cumulative Frequency

cumulative frequency distribution example

The frequency is actually the number of times an observation occurs for a particular time period. For example, in the class interval of 311-320, the actual value of the two observations is 312 and 319. What is the CDF of normal distribution in r? It is done by adding the frequency of the first class interval to the second class interval and both of them to the frequency of the third class interval and so on till the end. Step 4: The cumulative frequency column lists the total of each frequency added to its predecessor. In this type, the cumulate begins from the lowest to the highest size. Plot a less than type Ogive. How to enter a frequency table statistics? Draw an ogive for the following frequency distribution by less than method.

Next

What is cumulative distribution function with example?

cumulative frequency distribution example

How Many Types of Cumulative Frequency are There? This implies that the value of CF at any point can also not be greater than 1. The value of the point of intersection of both the curves gives the median of the given set of data. What is the first step in constructing frequency table? For example, 30 students are in 4 th grade or higher. Relative Cumulative Frequency Graph Relative cumulative frequency graphs are a type of ogive graphs that showcases the percentile of the given data. The records are as follows: 301, 312, 319, 354, 359, 345, 348, 341, 347, 344, 349, 350, 325,323, 324, 328,322, 332, 334, 337.

Next

Cumulative Frequency Distribution: Types, Graph using Examples

cumulative frequency distribution example

The y-axis of the bars shows the frequencies or relative frequencies, and the x-axis shows the values. It is obtained by summing up the probability density function and getting the cumulative probability for a random variable. This is the principle on which PDF itself is based, and this is the only essential requirement or condition that it requires. There are two types of Cumulative Frequency Curves or Ogives : More than type Cumulative Frequency Curve and Less than type Cumulative Frequency Curve. Cumulative Frequency Distribution: Definition The cumulative frequency will be calculated by adding each frequency from a frequency distribution table to its predecessors. A table that displays the cumulative frequencies that are distributed over various classes is called a cumulative Example 1: Robert is the sales manager of a toy company. A frequency distribution is a tabular representation of a survey data set used to organize and summarize the data.

Next