Decimal fraction to binary. how to convert negative fraction decimal to binary 2022-12-22

Decimal fraction to binary Rating: 7,6/10 1235 reviews

Decimal fractions, also known as decimal numbers or base-10 numbers, are numbers that are expressed using the base-10 numbering system, which consists of the digits 0 through 9. On the other hand, binary fractions, also known as binary numbers or base-2 numbers, are numbers that are expressed using the base-2 numbering system, which consists of only the digits 0 and 1.

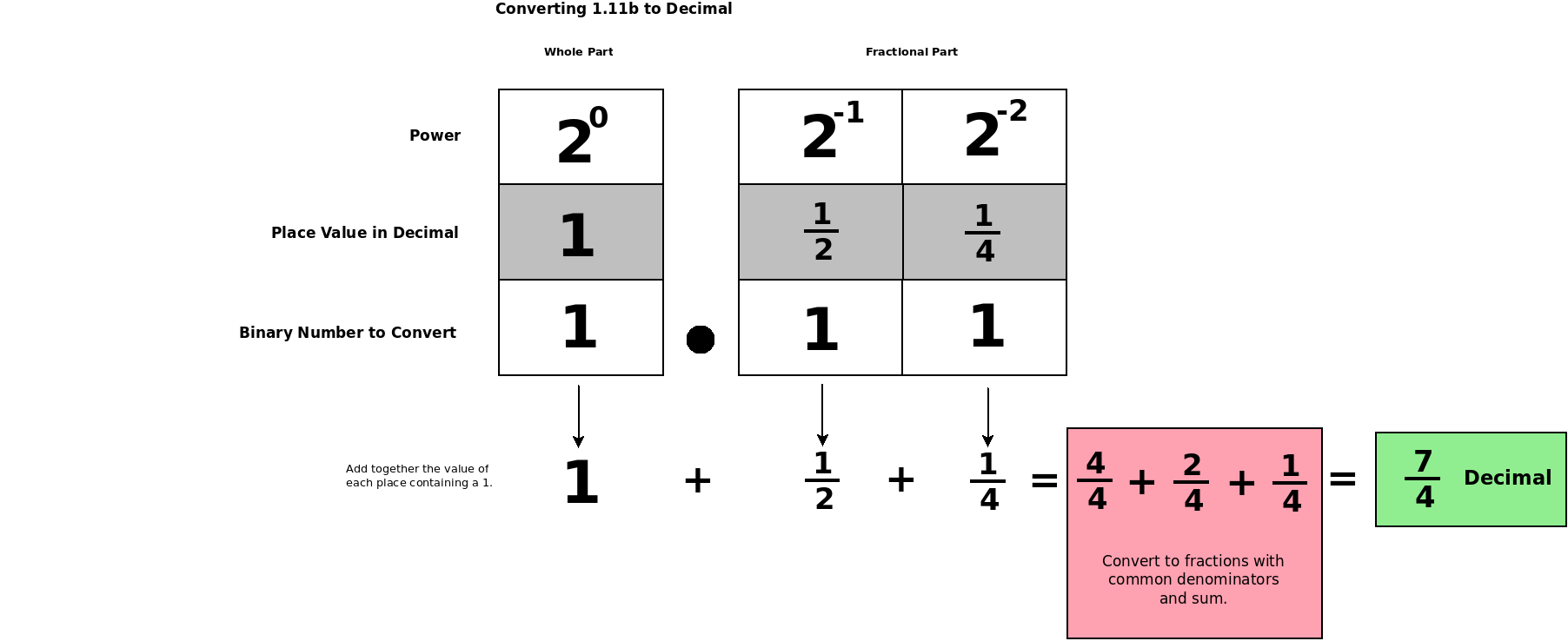
Converting a decimal fraction to a binary fraction may seem like a difficult task, but it is actually a fairly straightforward process once you understand the basic principles behind it. To begin with, it is important to understand that the place values in a binary number are based on powers of 2, rather than powers of 10 as in the case of decimal numbers. This means that the place value of each digit in a binary number is determined by the power of 2 that is associated with its position in the number. For example, in the binary number 1001, the digit 1 in the ones place has a place value of 1, the digit 0 in the twos place has a place value of 2, the digit 0 in the fours place has a place value of 4, and the digit 1 in the eights place has a place value of 8.

To convert a decimal fraction to a binary fraction, you will need to follow a few simple steps. First, you will need to determine the integer part of the decimal fraction. This can be done by simply taking the whole number part of the decimal fraction and expressing it in binary form. For example, if the decimal fraction is 3.625, the integer part is 3, which can be expressed in binary form as 11.

Next, you will need to determine the fractional part of the decimal fraction. This can be done by subtracting the integer part from the decimal fraction and multiplying the result by 2. If the result is less than 1, you will need to write a 0 in the binary fraction and repeat the process with the new fraction. If the result is greater than or equal to 1, you will need to write a 1 in the binary fraction and repeat the process with the new fraction, which will be the result of subtracting 1 from the previous result. You will need to repeat this process until the fractional part of the decimal fraction is reduced to zero or until you have reached the desired level of precision.

For example, to convert the decimal fraction 3.625 to a binary fraction, we can follow the steps outlined above as follows:

  1. Determine the integer part: 3.625 (decimal fraction) - 3 (integer part) = 0.625 (fractional part)
  2. Multiply the fractional part by 2: 0.625 (fractional part) x 2 = 1.25
  3. Write a 1 in the binary fraction and repeat the process with the new fraction: 1. (binary fraction) .25 (new fraction)
  4. Multiply the fractional part by 2: 0.25 (fractional part) x 2 = 0.5
  5. Write a 0 in the binary fraction and repeat the process with the new fraction: 10. (binary fraction) 0.5 (new fraction)
  6. Multiply the fractional part by 2: 0.5 (fractional part) x 2 = 1
  7. Write a 1 in the binary fraction and repeat the process with the new fraction: 101. (binary fraction) 0 (new fraction)

At this point, the fractional part of the decimal fraction has been reduced to zero, so we can stop the process. The final result is the binary fraction 11.101, which is the binary equivalent of the decimal fraction 3.

[PDF Notes] Conversion of Decimal fraction to Binary fraction 2023

decimal fraction to binary

Decimal Number System Definition The decimal number system employs 10 symbols to represent numbers with a base of ten: 0, 1, 2, 3, 4, 5, 6, 7, 8, and 9. So now we have. The next step is to flip all the bits, which means change the zero's to one's and vice versa; 10101. In this article, you are going to learn the conversion of decimal to binary number systems along with the conversion steps and examples. You should double-check our result by expanding the binary representation. These binary numbers are majorly used in computer applications, where it is used for programming or coding purposes. This leads to the existence of two zeros, one positive and one negative, which some mathematical people insist is proof positive that computer scientists shouldn't be trusted with math :- More detail can be found at It is a relatively simple operation to convert a negative decimal base-10 number to binary base-2.

Next

Omni Calculator logo

decimal fraction to binary

The whole number part of this new result is the secondbinary digit to the right of the point. Step 2: Next we disregard the whole number part of the previous result 0 in this case and multiply by 2 once again. If digit N+1 is a one, you need to round up since digits in binary can only be a 0 or 1, truncating with the next digit a 1 is as inaccurate as truncating a 5 in decimal. Every binary fraction has an exact decimal fraction equivalent. I'll take -10 for example. Step 3: Disregarding the whole number part of the previous result this result was. The whole number part of the result is now the next binary digit to the right of the point.

Next

Decimal fraction conversion to binary

decimal fraction to binary

Step 5: We multiply by 2 once again, disregarding the whole number part of the previous result a 1 in this case. First find the binary representation of positive 5. All the decimal numbers have their equivalent binary numbers. If the whole integer part is 1, note the one then remove the one and continue this process. We will continue this process until we get a zero as our decimal part or until we recognize an infinite repeating pattern. You can check this at the source provided.

Next

Converting Decimal Fractions to Binary

decimal fraction to binary

Binary Number System Definition The binary number system is a base-2 number system in which numbers are only represented by two digits: 0 and 1. You can continue adding more and more digits, so the answer would be 0. I want to determine how many exact binary bits are required to reconstruct the fraction from its floating point binary value. Now take the numbers we got and place them after the decimal point in the order we got them. All we have to do now is convert the binary fraction part.

Next

Decimal to Binary (Definition, Conversion, Table and Examples)

decimal fraction to binary

The same holds when you consider a number written in positional notation when you specify the position of a digit in a number. Now to answer your specific question Multiply 0. First you can consider the negative number as positive. That is why you get the digits in the opposite order, lowest first. This is just an example, I am looking to perform operations on large fractions with many digits e.

Next

How to convert binary fraction to decimal

decimal fraction to binary

Each time you multiply by 2, you are shifting the binary representation of the number left 1 place. Get a better understanding of your computer with us. Hence the representation of. Because 2 is a factor of 10, all binary fractions can be expressed as decimal fractions. Now, let us convert the given decimal number 294 into a binary number. This is because computers understand the language of binary digits, o and 1.

Next

Decimal to Binary Converter

decimal fraction to binary

So far, we have. Renew multiplying the resultant fractional part by 2 until we get a resulting fractional part equal to zero. We are then bound to repeat steps 2-5, then return to Step 2 again indefinitely. Continue this process until we get the quotient becomes 0. I will now demonstrate with a simpler result.

Next

how to convert negative fraction decimal to binary

decimal fraction to binary

To learn more, see our. . But I continued to show the repetition for clarity. Step 4: By placing all the remainders in order in such a way, the Least Significant Bit LSB at the top and Most Significant Bit MSB at the bottom, the required binary number will be obtained. The above figure shows the conversion of a decimal number 100 to binary.

Next