Bernoulli's principle is a fundamental concept in fluid mechanics that states that as the velocity of a fluid increases, the pressure within the fluid decreases. This principle is named after the 18th-century Swiss mathematician Daniel Bernoulli, who described it in his book "Hydrodynamica."
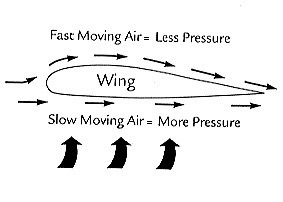
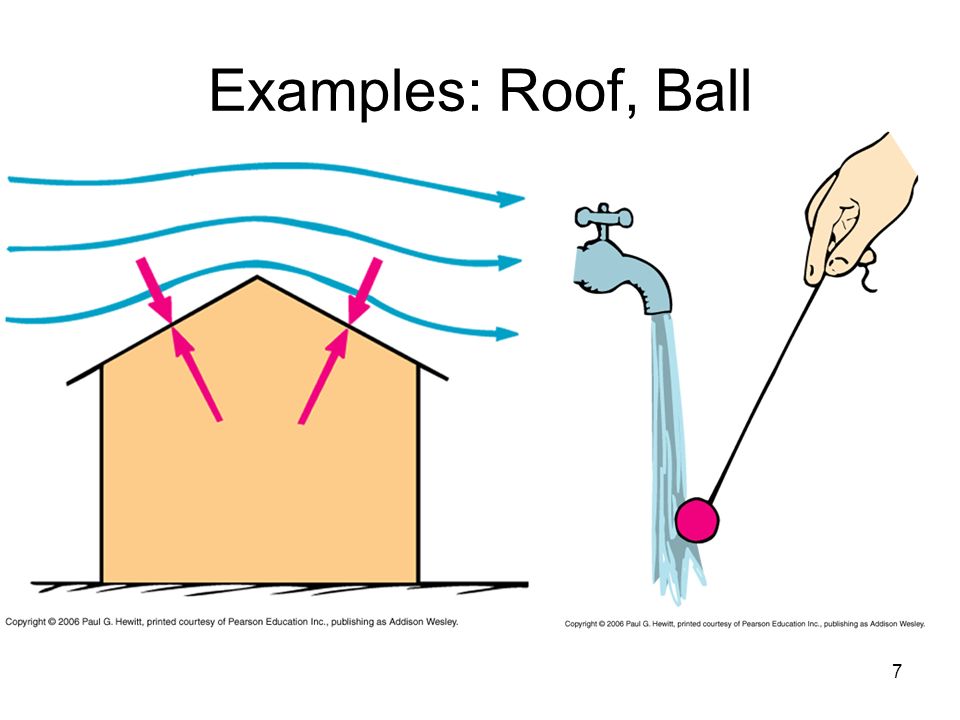
There are many examples of Bernoulli's principle in action in the natural world. One of the most familiar examples is the way that airplane wings are designed to lift the plane off the ground. The shape of the wing is carefully crafted so that the air flows faster over the top of the wing than it does underneath. This difference in velocity creates a difference in pressure, with the pressure being lower on the top of the wing. The resulting pressure difference generates an upward force, known as lift, that helps the plane to take off and stay airborne.
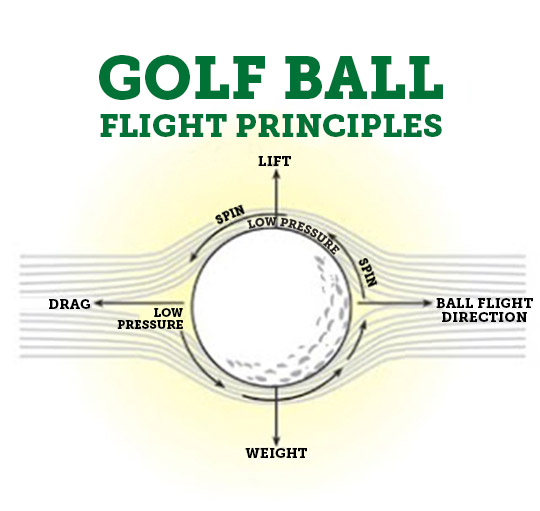
Another example of Bernoulli's principle can be seen in the way that a baseball curves as it travels through the air. When a pitcher throws a curveball, they apply a force to the ball that causes it to spin. This spin causes the air to flow faster over one side of the ball than the other, creating a difference in pressure that causes the ball to curve in the direction of the lower pressure.
Bernoulli's principle also plays a role in the operation of hydroelectric power plants. In these facilities, water is directed through a series of turbines, which use the kinetic energy of the flowing water to generate electricity. The pressure of the water decreases as it passes through the turbines, which helps to extract more energy from the flow.
In conclusion, Bernoulli's principle is a fundamental concept in fluid mechanics that helps to explain how fluids behave under different conditions. It has many practical applications, including in the design of airplane wings, the movement of baseballs, and the operation of hydroelectric power plants.
Bernoulli's Principle Applications & Examples
In essence, the theorem states that when the speed of an object moving through a fluid increases, it creates a decrease in the pressure exerted by the fluid on the object. As the ball spins, the surface friction of the ball with the surrounding air drags a thin layer referred to as the boundary layer of air with it. A thin layer of air is present around the ball as it rotates. Markings in a train platform are present to protect the passengers. With numerical data, the distribution will order the data from lowest to highest value. Likewise, the pressure in the fluid increases as the water slows down in the wider regions. Practically,it is not true.
Bernoulli’s Theorem and Its Applications
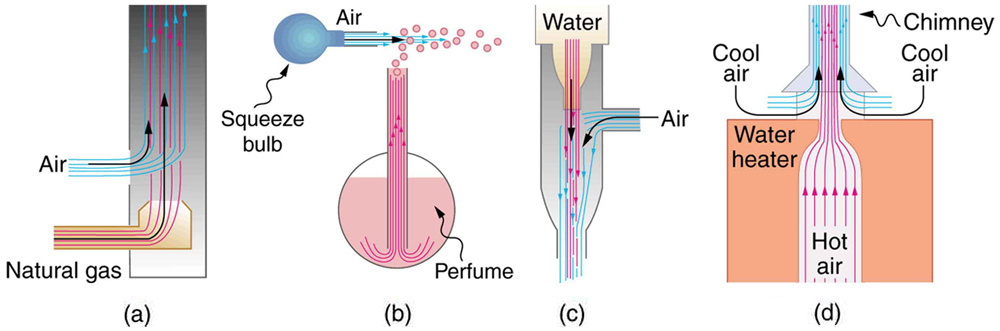
Lee Johnson is a freelance writer and science enthusiast, with a passion for distilling complex concepts into simple, digestible language. The entrainment of air in the fuel helps improve combustion. This is why Bernoulli's equation simply applies the conservation of energy in the fluid flow. However, it can be applied to unsteady flow if the fluid speed is small enough and the fluid density is constant. Thus, we can easily understand why chimneys work better when there is high wind flow.
Applications Of The Bernoulli's Principle
For example, submarines need navigational information for speed and stealth to avoid attacks by enemy submarines. You get the idea. This is equivalent to stating that there are no convective forces acting on the flowing fluid, i. The sharp fall in pressure sucks in more air which leads to more fuel being drawn in. It is important to consider the properties of the fluid, the shape and size of the object, and the flow conditions when applying the Bernoulli principle to a specific problem or situation.
Bernoullis Principle

The law was discovered by and named after the Italian scientist Evangelista Torricelli, in 1643. The fluid is accelerated as it passes through a narrow constriction in the venturi. Streamlines are far apart when the area surrounding the fluid is wide. A high-speed stream of fluids creates a low-pressure region, while the steady air creates a high-pressure region. The Bernoulli principle states that a region of fast flowing fluid exerts lower pressure on its surroundings than a region of slow flowing fluid. For example, it ensures safety, as flying too fast can cause the plane to shatter.
What are 2 examples of Bernoulli's principle? [Expert Guide!]

Bernoulli's principle explained the inverse relationship between pressure and fluid velocity, wherein the speed is high when the pressure is low and vice versa. In very simplistic terms, a Bernoulli distribution is a type of binomial distribution. However, this assumption is not always valid, particularly at high speeds or high altitudes where the effects of compressibility become significant. This is regardless of whether you are moving or standing still. DOE Fundamentals Handbook, Volume 1, 2 and 3. This means the flow speed is higher on the convex side than the concave side making the pressure lower. Bernoulli's principle has numerous applications in fluid dynamics.