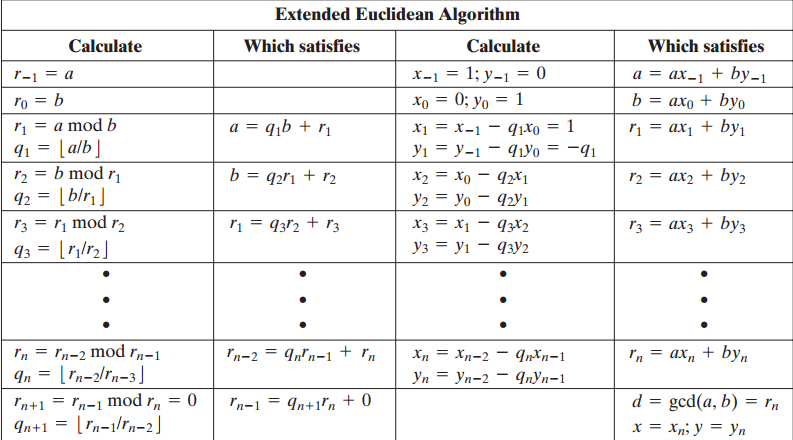
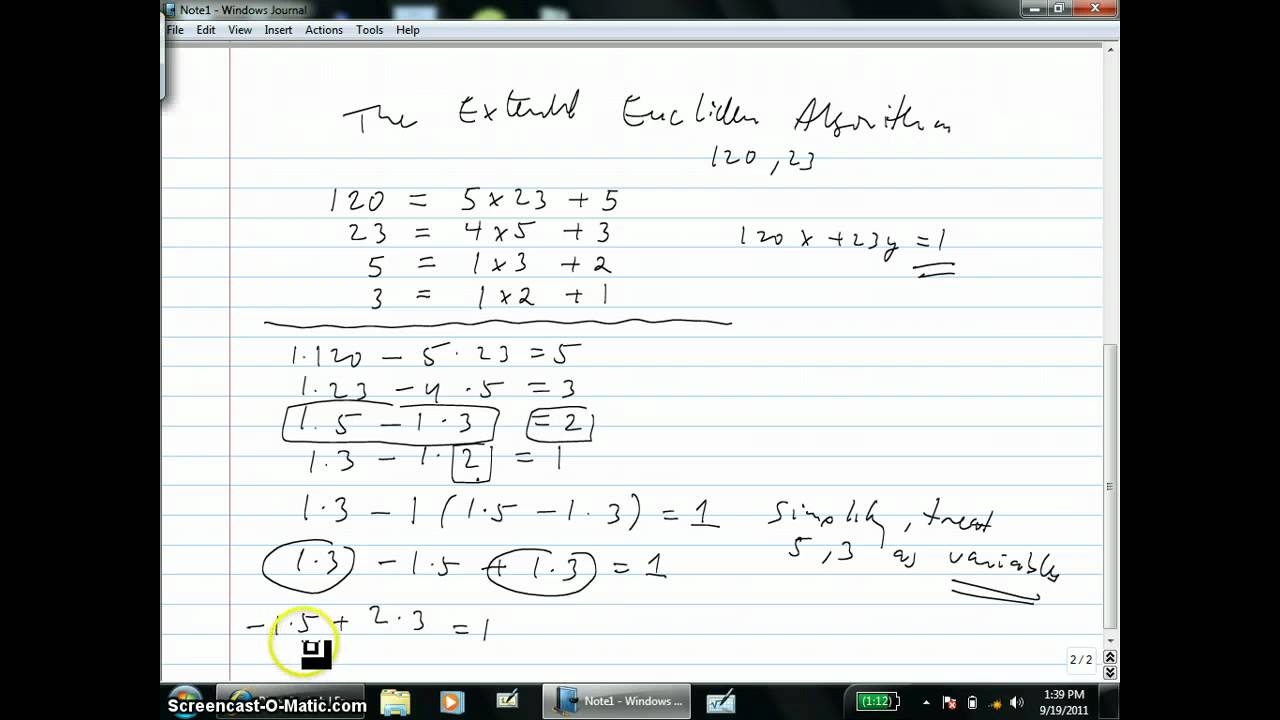
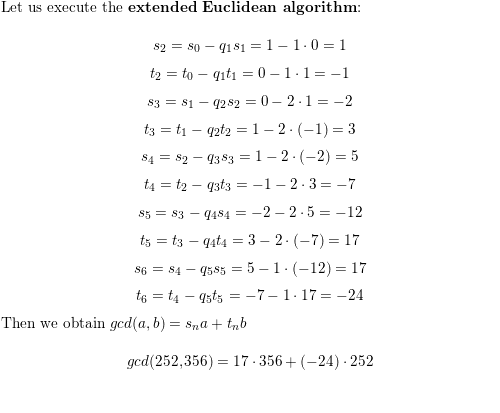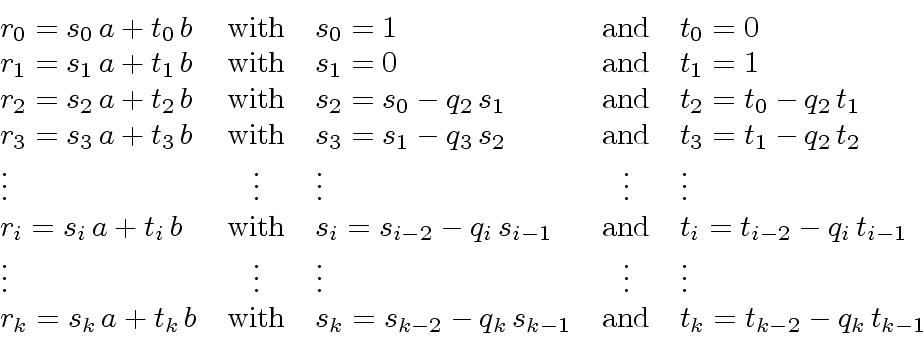Extended euclidean algorithm code. Extended Euclidean algorithm 2022-12-25

Extended euclidean algorithm code Rating: 4,6/10 1215 reviews

The extended Euclidean algorithm is an efficient method for finding the greatest common divisor (GCD) of two integers, as well as finding integers that satisfy the equation

ax + by = gcd(a, b)

where a and b are the input integers and x and y are the integers we wish to find. This equation is known as the Bézout's identity, and the integers x and y are known as Bézout coefficients. The extended Euclidean algorithm can be implemented in any programming language, and in this essay, we will discuss an implementation in the C programming language.

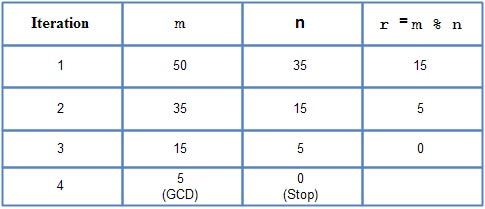
To begin, let's consider the basic Euclidean algorithm for finding the GCD of two integers. The algorithm works by repeatedly applying the division algorithm until the remainder is 0, at which point the divisor is the GCD. For example, to find the GCD of 24 and 16, we can perform the following steps:

24 / 16 = 1 remainder 8 16 / 8 = 2 remainder 0

Therefore, the GCD of 24 and 16 is 8.

The extended Euclidean algorithm builds upon this basic algorithm by also keeping track of the Bézout coefficients as the algorithm progresses. We can do this by using a recursive function that takes in the two input integers and two variables for the Bézout coefficients. Let's call this function extendedEuclidean().

Here is the basic outline of the extended Euclidean algorithm implemented in C:

int extendedEuclidean(int a, int b, int *x, int *y) {
    if (a == 0) {
        *x = 0;
        *y = 1;
        return b;
    }
    int gcd = extendedEuclidean(b % a, a, y, x);
    *y -= (b / a) * (*x);
    return gcd;
}

The function takes in the two input integers a and b, as well as pointers to the variables x and y that will be used to store the Bézout coefficients. The function first checks if a is 0, in which case it sets x to 0, y to 1, and returns b. This is the base case of the recursive function, and it allows the algorithm to terminate when the remainder is 0.

If a is not 0, the function calls itself with the arguments b % a and a, and assigns the result to the variable gcd. The function then subtracts (b / a) * x from y and returns gcd.

This may seem a bit confusing at first, so let's walk through an example to see how the algorithm works. Let's find the GCD of 24 and 16, as well as the Bézout coefficients, using the extended Euclidean algorithm.

We start by calling extendedEuclidean(24, 16, x, y). Since a is not 0, the function calls itself with the arguments extendedEuclidean(16, 24, y, x). This call returns the GCD of 16 and 24, as well as the Bézout coefficients y and x.

The function then calls itself with the arguments extendedEuclidean(8, 16, y, x). This call returns the GCD of 8 and 16, as well as the Bézout coefficients

Euclidean algorithms (Basic and Extended)

extended euclidean algorithm code

Even though this is basically the same as the notation you expect. What will you find here? That's why we now return abs a instead of abs b. But after r becomes 0, we're still assigning new values to a and b. This video covers the same material as this page, so you don't have to watch it if you already read this page Unless you feel like you need to understand it better. We've hidden all of the codes inside spoilers to make the page look better. If b does not have a multiplicative inverse mod n, then throw an exception.

Next

Python and C++ code for the Extended Euclidean Algorithm

extended euclidean algorithm code

Well, because it allows us to calculate some extra things. There are several ways to define unambiguously a greatest common divisor. Calculate gcd a, b and s and t. Otherwise, one may get any non-zero constant. When using integers of unbounded size, the time needed for multiplication and division grows quadratically with the size of the integers. But there's a small problem: s × a + t × b can result in a negative number e.

Next

The Extended Euclidean Algorithm explained with examples

extended euclidean algorithm code

If b does not have a multiplicative inverse mod n, then throw an exception. Home Welcome on ExtendedEuclideanAlgorithm. The reason that this happens is because we always skip the last row in our version of the Euclidean Algorithm because we're lazy. So to solve this, we can just include the row that we always skip in our algorithm. Just add 1 0 1 0 1 to the table after you wrote down the value of r.

Next

Extended Euclidean Algorithm

extended euclidean algorithm code

Don't just head over the calculator right away, because I understand that it may seem weird and intimidating when you see its first output. Why do we need the Extended Euclidean Algorithm at all? Do you want to know what a table looks like that doesn't skip the last row? So for the first row in the table, we can always write down a 1 for s3. Do you want to practice more? Let's add this value to the table to finish the first row: a b q r s1 s2 s3 t1 t2 t3 161 28 5 21 1 0 1 0 1 -5 Now the first row is done! After that it's easier to understand the recursive version, which you can then use for your homework or project. As seen above, x and y are results for inputs a and b, a. So our calculation is correct. But when b already equals 0 at the start, this extra row is actually the only row in the table. } Otherwise, everything which precedes in this article remains the same, simply by replacing integers by polynomials.

Next

C Program for Extended Euclidean algorithms?

extended euclidean algorithm code

Since 1 is the only nonzero element of GF 2 , the adjustment in the last line of the pseudocode is not needed. If you want to read more about this, check the information inside the spoiler Extended Euclidean Algorithm recursive This is the same as the recursive code for the Euclidean Algorithm, but with some extra lines. Luckily we can check whether we have done it correctly. If that succeeds, verify that it's correct. The mod operator of C++ doesn't handle that well.

Next

C++ Program to Implement Extended Euclidean Algorithm

extended euclidean algorithm code

We try to calculate the modular multiplicative inverse. For the Python code, we return s, t and the absolute value of b. Or are you just very lazy? What values can we copy? We write down everything we need and skip all the things we don't need to write down. In this extra row, b from the previous row has been copied into a again, r into b, s2 into s1, s3 into s2, t2 into t1 and t3 into t2. To adapt the extended Euclidean algorithm to this problem, one should remark that the Bézout coefficient of n is not needed, and thus does not need to be computed.


Next

Extended Euclidean Algorithm Calculator

extended euclidean algorithm code

If that happens, don't panic. Even if you edit the code or translate it to another programming language, do not get rid of the link to this webpage inside the code. Please have a look at the Enjoy and good luck studying! Take a deep breath, it's al going to be okay. An exception will occur, since 15 mod 10 does not have a modular multiplicative inverse. Here we've fixed that as well with a simple if statement. This is how the calculator displays the output: a b q r s1 s2 s3 t1 t2 t3 15 0 - - 1 0 - 0 1 - So here the "extra" row in the table is the only row in the table. You may have seen some already that require things like backwards substition or to write "gcd.

Next

Extended Euclidean algorithm

extended euclidean algorithm code

Remember what the table looked like?. Basic Euclidean Algorithm for GCD: The algorithm is based on the below facts. Have a look at this overview. Everything put together into one program We've put all of the functions discussed on this page in a single file for, such that you can play with it. } Thus t, or, more exactly, the remainder of the division of t by n, is the multiplicative inverse of a modulo n. So if we decide to omit it, we have a table with no rows. The Extended Euclidean Algorithm Explained step-by-step with examples.

Next

Extended Euclidean Algorithm

extended euclidean algorithm code

That is what the extra columns are for. If it doesn't succeed, show the error raised by the function. If b does not have a multiplicative inverse mod n, then throw an exception. You can also do this with return statements. The extended Euclidean algorithm is particularly useful when a and b are coprime or gcd is 1. That's why we raise Python or throw C++ an exception when there is no modular multiplicative inverse.


Next